Toetsen op samenhang en verschil
| Inleiding | Chi-square toets | Independent Sample T-test | Pearson PM toets |
|---|
Chi-Square.
De Chi-Square toets pas je toe op twee nominale of ordinale variabelen. De Chi-Square hangt nauw samen met de Crosstab.
Bij de paragraaf van de Crosstab hebben we gekeken naar het verband tussen bv het geslacht en burgerlijke staat. Hier kwam de volgende tabel uit:
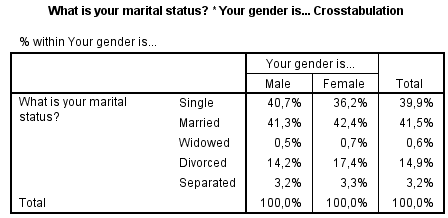
In de tabel zie je dat er een klein verschil is tussen mannen en vrouwen. De tabel is tot stand gekomen door analyse van gegevens uit een steekproef. Bij het trekken van de steekproef speelt het toeval altijd een grote rol. De vraag is hoe groot die rol is en of we dit ook kunnen berekenen. In het onderdeel statistiek wordt dit voor een groot deel gedaan. In de berekening werd gebruik gemaakt van het verschil tussen verwachte en geobserveerde waarde. Dit kan SPSS uitrekenen door met de residuen te rekenen, zoals we gezien hebben.

Door het residu te kwadrateren en vervolgens te delen door de verwachte waarde, daarna op te tellen en de uitkomst daarvan weer in een tabel op te zoeken (zoals we gezien hebben in het theorie gedeelte statistiek), is het mogelijk te kijken of er een daadwerkelijk verschil is.
SPSS pakt het voor ons iets eenvoudiger aan. De berekening die achter de schermen wordt uitgevoerd is veel lastiger, maar dat zal ons een zorg zijn. We kunnen de Chi-Square laten uitrekenen en wel als volgt
Ga naar het Crosstab scherm:
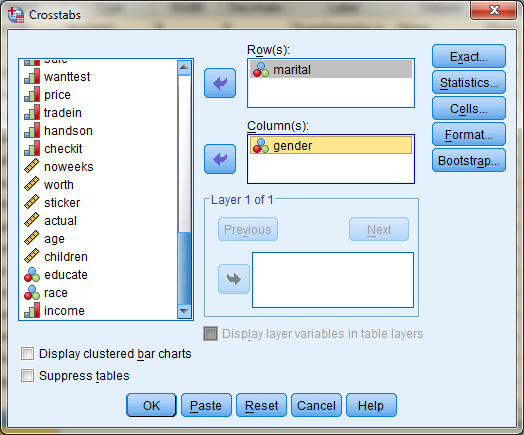
Zorg dat je door de Cells in te vullen de percentages in de kolommen plaatst.
klik daarna op de Statistics Knop.
Je komt in het volgende scherm:
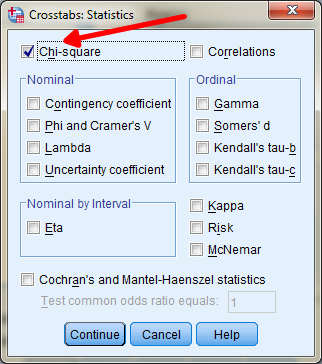
Klik bovenaan Chi-square aan. Klik vervolgens op Continue en op Ok. Het resultaat moet zijn:
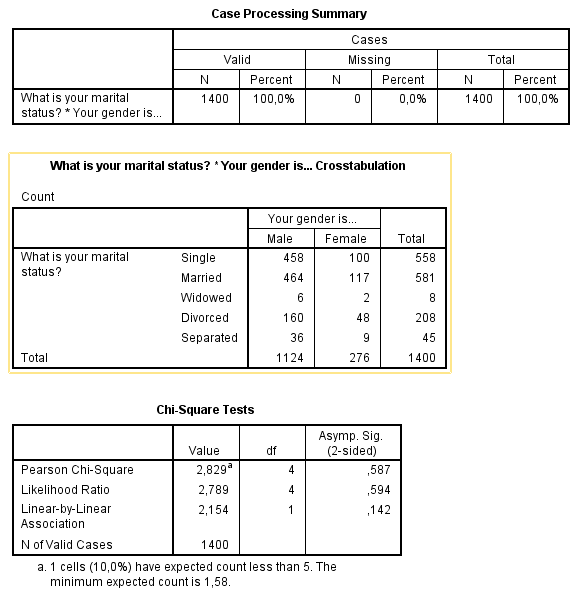
Voor de Chi-Square toets maken wij gebruik van de Pearson Chi-Square.
Je ziet dat het aantal vrijheidsgraden 4 is ((2-1)*(5-1)).
De waarde die berekend wordt is 2,829 (deze wordt op een andere manier berekend dan wij binnen statistiek doen).
De kolom "Asymp. Sig (2 sided)" is wel van groot belang, en de interpretatie van beide tabellen is de volgende:
De Ho Hypothese is dat er geen verschil in burgerlijke staat is tussen mannen en vrouwen (natuurlijk binnen de populatie van Auto-Online lezers).
Uitgaande dat de Ho hypothese waar is, is de kans dat bij een steekproef de waarden uit komen zoals ze in de tabel met percentages staan, 58,7% (Aymp. Sig). Die kans is dus erg groot. Dus waarschijnlijk is het uit de tabel af te lezen verschil in burgerlijke staat tussen mannen en vrouwen, gebaseerd op gewoon toeval.
Wanneer zeggen we dat het geen toeval is. Als de kans dat het optreedt heel klein is. Heel klein wil zeggen kleiner dan 5% (het significantie niveau), en soms wel nog kleiner als we het significantie niveau op 1% stellen.
Het volgende voorbeeld laat zien wat er in de tabel staat als er wel sprake is van een significant verschil.
In het voorbeeld van de Crosstabs hebben we ook gekeken of er een verschil is in hoe vaak men inkopen doet via internet en het geslacht. We kunnen daar de volgende tabellen voor maken. Doe dat.
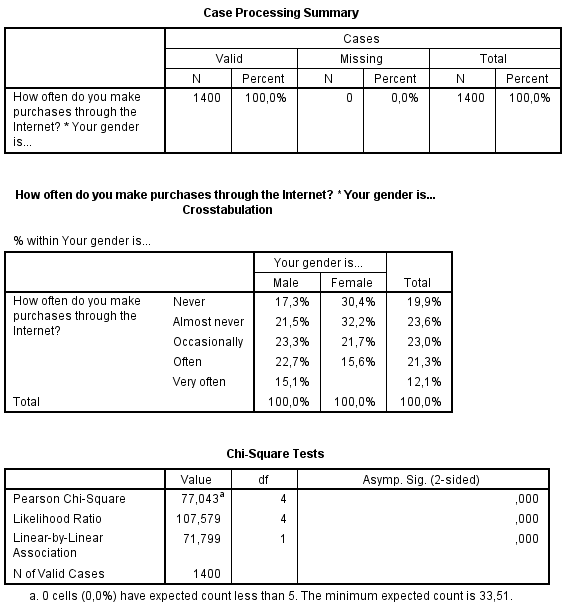
De Ho Hypothese is dat er geen verschil is in hoe vaak men inkopen doet op internet tussen mannen en vrouwen.
Te zien is dat de Asymp.Sig 0,00 is. Dit lijkt nul, maar is het niet. Door er een paar keer op te klikken en een andere notatie te kiezen zie je dat de volgende waarde die heel erg klein is.
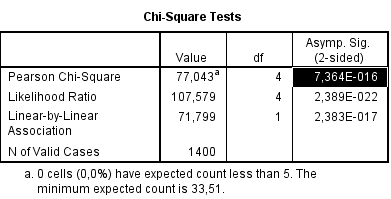
Wat wil dit nu zeggen:
De kans uitgaande van het feit dat er geen verschil is tussen mannen en vrouwen in het aantal keren dat men op internet koopt, en de gevonden uitslag in de tweede tabel, is bijna nul (heel en heel klein). Als die kans dan zo klein is, dan is het niet waarschijnlijk dat de aanname de Ho ook daadwerkelijk waar is. In dat geval wordt Ho verworpen.
De uitspraak is dat er en significant verschil is in hoeveelheid aankopen tussen mannen en vrouwen bij een significantie niveau van 5%.
Het begrip significantie is een heel lastig begrip en wordt verder uitgelegd bij het onderdeel statistiek.
Is niet duidelijk hoe je het een en ander doet, bekijk dan onderstaand filmpje.
| Inleiding | Chi-square toets | Independent Sample T-test | Pearson PM toets |
|---|