Analyse samenhang en verschil
| Crosstabs | Tables | Stacked Bar | Histogram | Boxplot | Special Stacked Bar |
|---|
Crosstabs.
De kruistabel wordt veel gebruikt bij verschil of samenhang vragen. Een voorbeeld van samenhang is te kijken of er een verband is tussen het opleidingsniveau van iemand en zijn arbeidsniveau. Een voorbeeld van een verschil vraag is de vraag of er een verschil is in het geslacht (man of vrouw zijn) en het arbeidsniveau waarop men werkt. Bij verschil en samenhang vragen speelt het meetniveau weer een grote rol.
Als het meetniveau van beide variabelen nominaal of ordinaal is, wordt gebruik gemaakt van de kruistabel techniek.
Stel we willen weten of er onder respondenten van de Auto-online een verschil is tussen mannen en vrouwen wat betreft hun burgerlijke staat. Het geslacht wordt hier de splitsingsvariabele genoemd, de burgerlijke staat de testvariabele.
Je komt in het scherm om de opties voor de kruistabel in te stellen door te kiezen voor: Analyze --> Descriptive Statistics --> Crosstabs.
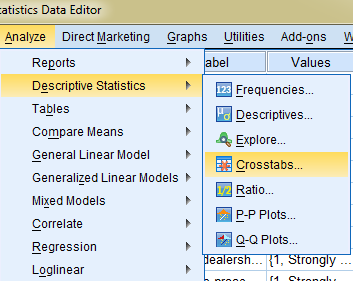
In de rijen en kolommen kun je de variabelen plaatsen. Mijn voorkeur gaat er naar uit om de splitsingsvariabele altijd in de kolommen te plaatsen. Ik zal dat iets verderop toelichten.
Stel het Crosstabs scherm als volgt in.
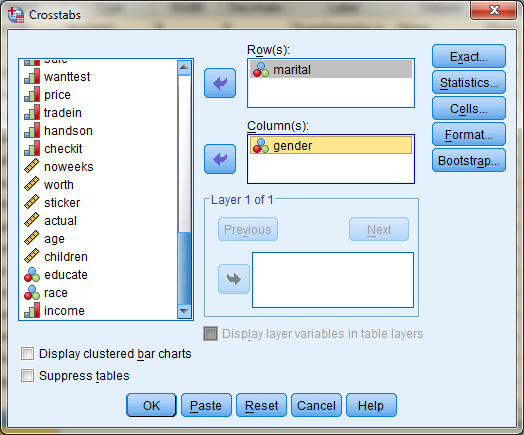
Klik dan op Ok. Je krijgt de volgende outputtabel:
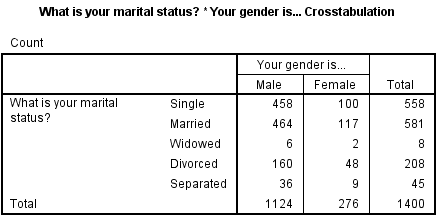
Omdat in deze tabel met aantallen gewerkt wordt, kan ik nog weinig zeggen over enig verschil. Zou ik met percentages werken, dan kan ik misschien wel meer conclusies trekken. Ik moet mijn percentages dan wel goed kiezen. Dit doe je als volgt:
Omdat je het verschil tussen mannen en vrouwen wilt aantonen zou je kunnen gaan kijken hoeveel procent van zowel de mannen als de vrouwen alleenstaand, getrouwd, weduwe of gescheiden zijn. In mijn tabel zou dan helemaal onderaan bij Totaal, voor zowel de mannen, vrouwen 100% moeten komen te staan. Dat wil zeggen dat ik mijn percentages zo moet instellen dat de kolommen samen 100% zijn. Je doet dit als volgt.
Ga eerst weer terug naar je Crosstabs venster. Laat de variabelen Marital en Gender gewoon staan. Kies voor de optie "Cells " om in onderstaand scherm te komen. Klik Observed uit, en onder percentages Colums aan.
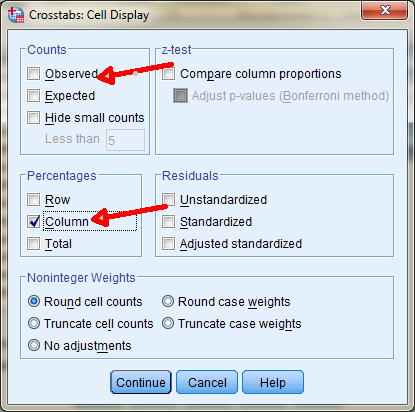
Klik daarna Continue en op Ok om de tabel te laten zien.
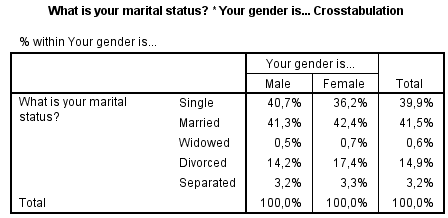
Lees de tabel van boven naar beneden, dus "van de mannen die meegedaan hebben aan deze enquête is 40,7% alleen, 41,3% getrouwd enz". "Van de vrouwen is 36,2% alleen, 42,4% getrouwd enz."
Ook kun je zien dat van alle respondenten van de enquête 39,9% alleen is, 41,5% getrouwd enz.
De conclusie is dat er een verschil is tussen mannen en vrouwen, maar dat verschil is wel erg klein. Of het groot genoeg is zien we straks met de Chi-Square test.
Want tot nu toe hebben we geen rekening gehouden met het feit dat het om een steekproef gaat en dat het niet de hele populatie Auto-Online lezers betreft.
Bij een steekproef kan het aan de toevalligheid van het nemen van de steekproef liggen dat er een verschil is. En we mogen dan niet met zekerheid stellen dat er een verschil is.
Mijn voorkeur om de "splitsings variabele" in de kolommen te zetten, komt voort uit het feit dat ik dan altijd percentages in de kolommen kan zetten. Vaak bestaat de "Splitsingsvariabele" uit minder waarden dan de "test variabele" dus qua lay-out komt het ook vaak beter uit. Maar het is geen vaste regel. Ik had net zo goed geslacht in de rijen kunnen zetten, en dan de percentages op Rijpercentage.
We gaan eerst wat dieper in op de mogelijkheden van de optie Crosstabs en de aansluiting op de statistiek theorie.
Als er geen verschil tussen mannen en vrouwen zou zijn, dan zouden de verdelingen van de mannen en vrouwen overeen moeten komen met de rechterkolom de totaalkolom. Dus 39,9% van de mannen, maar ook van de vrouwen zou alleenstaand moeten zijn.
Wat het zou moeten zijn noemen we de Expected Values, wat er staat zijn de Observed Values (zoals ook echt waargenomen. Dit kunnen we instellen in het Crosstabs: Cell Displays scherm, wat we al eerder gezien hebben. Stel dit als volgt in:
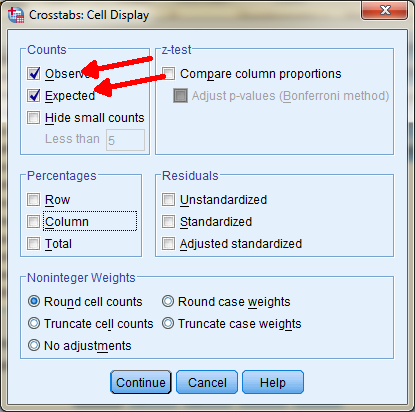
En klik op Continue en Ok zodat je onderstaande tabel krijgt.
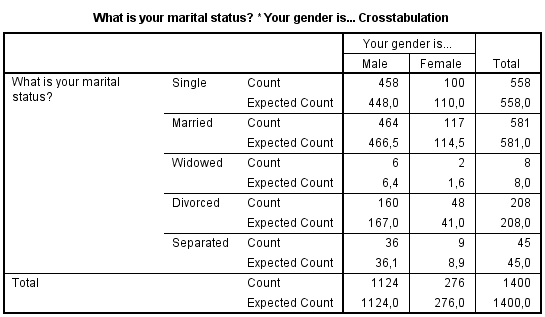
Je ziet dat Count het geobserveerde aantal is (stond ook in de eerste tabel). De Expected Count is het aantal wat je zou mogen verwachten als er geen verschil is tussen mannen en vrouwen (dit is voor alleenstaand 39,9% van 1124 is 448 voor de alleenstaande mannen en 39,9% van 276 is 110 voor de alleenstaande vrouwen. Als het verschil tussen de "geobserveerde waarde" en de "verwachte waarde" groot is, dan is een dus een verschil tussen de splitsingsvariabelen.
In het volgende voorbeeld gaan we bekijken of er een verschil is tussen hoe vaak men iets koopt op het internet en het geslacht. Maakt hiervoor zelf de volgende Crosstab.
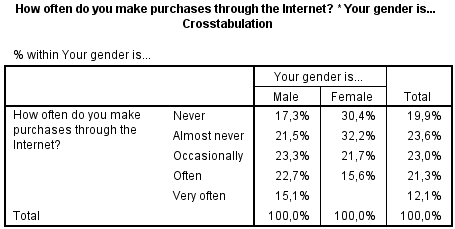
Op basis van deze tabel zou je kunnen zeggen dat mannen vaker hun inkopen via het internet doen.
We kunnen ook nog eens kijken naar geobserveerde en verwachte waarden.
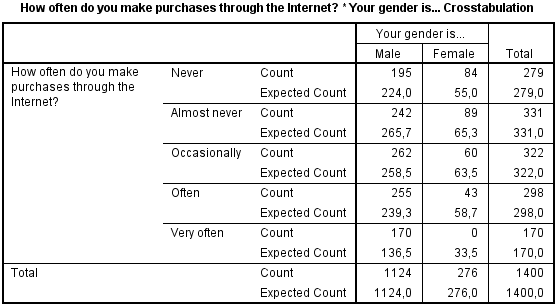
SPSS kan ook de verschillen laten zien tussen de geobserveerde waarden en Expected waarden.Het verschil is een residu. Stel daarom in het Croosstabs: Cells Display scherm "Unstandardized" in.
Je krijgt dan het volgende scherm.

Hierin zie je dat de verschillen tussen verwachte en geobserveerde waarden best groot zijn.
| Crosstabs | Tables | Stacked Bar | Histogram | Boxplot | Special Stacked Bar |
|---|