Enkelvoudige toetsen
| Inleiding | Binomiale toetsen | Chi-square toets | One-Sample T-test |
|---|
One Sample T-Test
De One sample T-test wordt gebruikt bij Scale variabelen om te toetsen of het gevonden gemiddelde overkomt met het verwachte gemiddelde. De One sample T-test kun je vinden in het menu onder:
Stel de redactie van Auto online denkt dat de gemiddelde leeftijd van de van de lezers van auto online 40 jaar is.
Analyse met SPSS Descriptive levert de volgende tabel op:

De vraag is nu of de aanname dat de leeftijd 40 was, verkeerd is. Dit geeft ons twee hypotheses:
H0: De gemiddelde leeftijd is 40 jaar.
H1: De gemiddelde leeftijd is niet gelijk aan 40 jaar.
Het vergelijken van de uitkomst van een analyse is een voorbeeld van de One-sample T Test. Kies hiervoor en je komt in het volgende scherm.
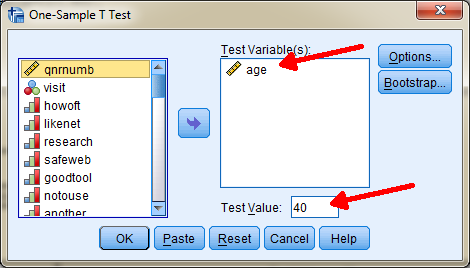
Voer de variabele Age in die je af gaat zetten tegen de test variable die de waarde 40 heeft. klik vervolgens op Ok en je krijgt de volgende uitkomsten.
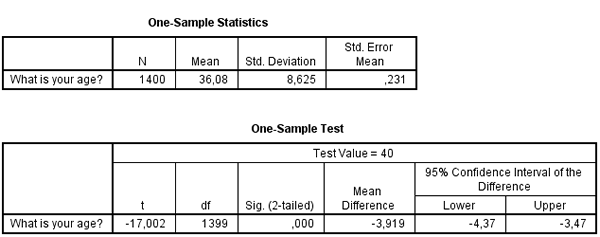
De bovenste tabel geeft waarden aan vergelijkbaar met die, die je krijgt bij Descriptives.
De onderste tabel berekent de t-waarde uitgaande van testwaarde 40. Op basis van die t-waarde en het aantal vrijheidsgraden wordt het significantie niveau uitgerekend. Deze is heel laag (staat afgerond onder Sig. (2-taled)) en in ieder geval kleiner dan 5% (het significantie niveau waar we gemakshalve nu maar van uitgaan). Dat wil zeggen dat we de H0 hypothese laten vervallen en ons uitgangspunt de gemiddelde leeftijd is 40 komt te vervallen.
In de tabel wordt ook het 95% betrouwbaarheidsinterval gegeven van een nieuwe variabele, "het verschil tussen de gemeten waarde en de waarde van de test variabele". (Dus van iedere leeftijd ingevuld door de respondent wordt 40 af getrokken. Van deze nieuw ontstane variabele wordt het gemiddelde uitgerekend. Dit is -3,919 met een 95% betrouwbaarheidsinterval van -4,37 en -3,47. Ga na dat omdat de waarde nul niet in dit interval valt, ik ook al had kunnen zeggen dat er een significant verschil is)
Een andere leuke vraag is de volgende. Zelden wordt er voor een auto de prijs betaald die op de verkoopstikker staat. Er wordt op afgedongen. Hoeveel gemiddeld kunnen we als volgt berekenen:
We laten SPSS een nieuwe variabele Verschil_Actueel_Sticket maken. Dit doen we in het menu Transform --> Compute variabele.
Voer de volgende formule in in het scherm dat je krijgt:
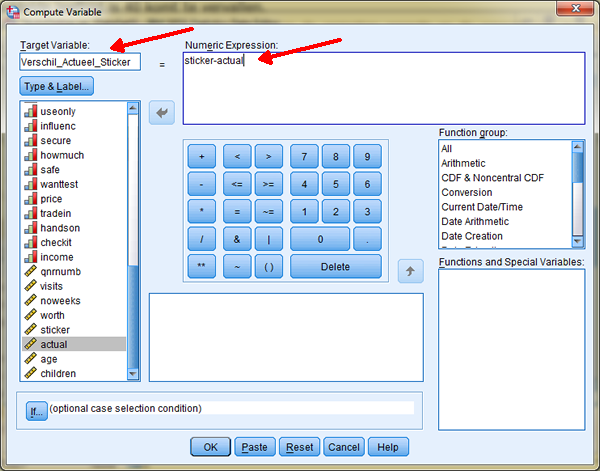
Klik op Ok.
Ga na in de variabele view dat er een nieuwe variabele met de naam "Verschil_Actueel_Sticker" aangemaakt is.
Geef deze variabele de label omschrijvingen "Bedongen op de sticker-prijs". Ga na dat dit de volgende tabel oplevert.

Volgens de branche vereniging wordt er normaal gesproken gemiddeld 15 % afgedongen. Wijkt nu de uitslag van de Auto online lezers hier significant vanaf.
Uitwerking. Er zijn meerder mogelijke uitwerkingen maar die van mij geeft het volgende resultaat.
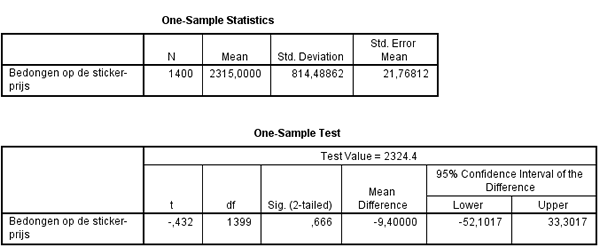
Daarbij is mijn conclusie dat er tussen de auto-online lezers en de gegevens van de branche vereniging geen verschillen zijn.
| Inleiding | Binomiale toetsen | Chi-square toets | One-Sample T-test |
|---|